Every Artificial Neural Network (ANN) has its own design for solving its problem most efficiently.
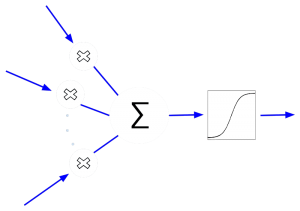
Artificial Neurons
ANNs imitate the human brain. Therefore, they consist of many artificial neurons.
Each neuron is designed to receive an input, process that input (and adjust its weights) and sends the processed input as output to the next neuron, as shown in figure 1.
Neural Network Topologies
The topology of an Artificial Neural Network (ANN) describes how all neurons in the network are connected.
The network is always structured in layers of neurons. The first layer represents an input, which is sent to all neurons in the following (‘hidden’) layer. From there on, the signals may travel through a vast number of hidden layers. In the end, the signals reach the output layer – meaning that they have been processed. If the network is already trained, the output should be the desired result. Depending on the number of hidden layers, the network is considered a ‘mono-‘ or ‘multi-layer’ network.
The signals in neural networks flow either in only one direction or appear in a higher frequency throughout the whole network. When signals flow in only direction, this network would be categorized as a feedforward neural network, as shown in figure 2.

Feedforward neural networks have been applied to a wide range of applications. The most common applications include curve fitting, pattern classification and nonlinear system identification. (cf. Tang, Huajin; Tan, Kay Chen; Zhang, Yi: ‘Neural networks : computational models and applications’, P. 1)
In recurrent neural networks, also known as feedback networks, the incoming signals do not flow into one direction. The network makes use of internal recurrence, as shown in figure 3. Recurrence is the act of feeding processed signals back into a neuron or hidden layer that has already received and processed this signal earlier. In that way, the neuron can adjust its weights earlier and therefore adapt easier. (cf. Soares, Fábio M.; Souza, Alan M.F.: ‘Neural Network Programming with Java’, P. 10)
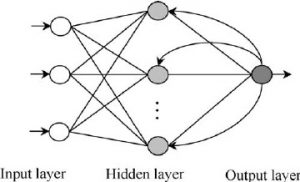
These networks show a great potential for applications in associative memory, optimization and intelligent computation. (cf. Tang, Huajin; Tan, Kay Chen; Zhang, Yi: ‘Neural networks : computational models and applications’, P. 2-4)
Neuro-Evolution
In traditional NE approaches, the network topology is usually a single hidden layer of neurons, with each hidden neuron connected to every network input and every network output (aka monolayer network).
The goal of NE is to optimize all neurons’ weights that determine the functionality of the network. This is done by applying crossover and mutation functions to selected weights within the network. If done right, evolving structure along with weights can significantly enhance the performance of NE.
NEAT – introduction
Neuro-Evolution of Augmenting Topologies (NEAT) is a NE method that is designed to take advantage of structure as a way of minimizing the dimensionality of the selected network fraction of weights. The learning speed of the network increases significantly with this method, due to the network growing through constant crossover operations on the one hand and the constant evolutionary minimization of the whole topology on the other. (cf. Stanly, Kenneth; Miikkulainen, Risto: ‘Evolving Neural Networks through Augmenting Topologies’, P. 3)